1. Elimine o módulo:
Dica:
-Definição de módulo:
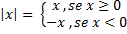
- Propriedades úteis:
i) |x| ≥ 0
ii) |x|² = x²
- Estudo do sinal de expressões na forma ax² - c:
a) Encontrar as raízes x1 e x2 da equação:
ax² - c = 0
ax² = c
x² = c/a
x = ± √c/a
Portanto a equação terá duas raízes inteiras de mesmo módulo e sinais diferentes. Assim, x1= √c/a e x2= - √c/a.
b) Graficamente:
Se a > 0 :
 ( Supondo x1 < x2 )
( Supondo x1 < x2 )Se a < 0:
 ( Supondo x1 < x2 )
( Supondo x1 < x2 ) - Estudo do de expressões na forma ax + b:

a) |-5| + |-2|
Solução:
Pela definição de módulo, temos:
|-5| = -(-5) = 5 , sendo -5 <0
|-2| = -(-2) = 2, sendo -2 < 0
Assim,
|-5| + |-2| = 5 + 2 = 7
b) |-5 + 8|
Solução:
Temos que :
|-5+8|=|3|
Pela definição de módulo:
|3| = 3 , pois 3 > 0
c) |-a|, a > 0
Solução:
Se a > 0, logo –a < 0, portanto pela definição de módulos, temos:
|-a| = - (-a) = a , pois -a < 0
c) |a|, a < 0
Solução:
Pela definição de módulo, temos:
|a| = -a , pois a < 0
d) |-a|
Solução:
Pela definição de módulo, temos:
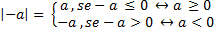
e) |2a| - |3a|
Solução:
Pela definição de módulo, temos:
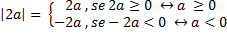
e
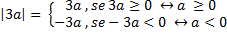
Assim,
-Se a ≥ 0:
|2a| - |3a| = 2a - 3a = -a
-Se a < 0:
|2a| - |3a| = -2a - (-3a) = -2a + 3a = a
Portanto,
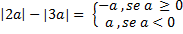
2. Resolva as equações.
a) |x|= 2
Solução:
Pela definição de módulo, temos:
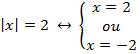
b) |x+1|=3
Solução:
Pela definição de módulo, temos:
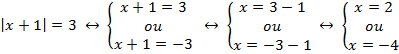
c) |2x-1|=1
Solução:
Pela definição de módulo, temos:
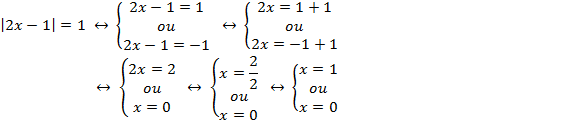
d) |x-2|=-1
Solução:
Não adimite solução pois |z| ≥ 0, para qualquer z, portanto |x-2| = -1 < 0 não é válido.
e) |2x+3|=0
Solução:
Pela definição de módulo, temos:
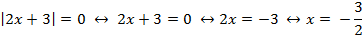
f) |x|=2x+1
Solução:
Pela definição de módulo, temos:
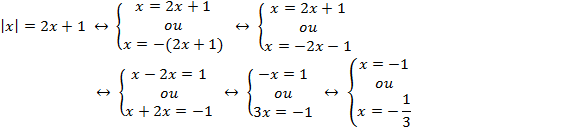
Substituindo:
|x|= 2.(-1) + 1 = -2 + 1 = -2 < 0
|x|= 2.
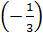 + 1 =
+ 1 = 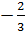 + 1 =
+ 1 = 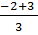 =
=  > 0
> 0Observe que se x = -1, o módulo resulta em um número negativo, portanto não é válido. Assim |x| = 2x+1 , somente para
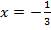 .
. 3. Resolva as inequações.
Dica :
- Definição de módulo:
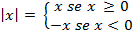
- Propriedades úteis:
i) |x| ≥ 0
ii) |x|² = x²
a) |x|≤ 1
Solução:
|x|² ≤ 1²
x² ≤ 1
x² - 1 ≤ 0
Estudando o sinal de x² - 1:
- Determinar as raízes da equação:
x² - 1 = 0
x² = 1
x = ± √1
x = ± 1
As raízes são : 1 e -1
-Graficamente:
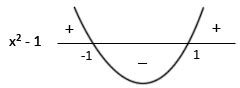
Portanto |x| ≤ 1 ⇔ x² - 1 ≤ 0 , para -1 ≤ x ≤ 1
b) |2x-1|< 3
Solução:
|2x-1|² ≤ 3²
(2x-1)² ≤ 9
4x² -4x +1 ≤ 9
4x² -4x +1-9 ≤ 0
4x² -4x -8 ≤ 0
Estudando o sinal de 4x² -4x -8:
- Determinar as raízes da equação:
4x² -4x -8 = 0
Dividindo todos os membros por 4, temos:
4x² -4x -8 = 0 ⇔ x² - x – 2 =0
Usando a Fórmula de Bkaskara, temos:
| Δ = (-1)²-4.1.(-2) Δ = 1+8 Δ = 9 |
Logo, as raízes da equação são : 2 e -1.
-Graficamente:
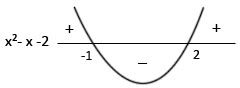
Portanto, |2x-1|< 3 ⇔ x² - x – 2 < 0 , para -1 < x < 2.
c) |3x-1| < -2
Solução:
Por (i) temos que |3x - 1| ≥ 0 para todo x, logo |3x-1| < -2 não está definido.
d) |3x-1|<

Solução:
|3x-1|² <
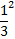
(3x-1)² <
9x² -6x +1 <
9x² -6x +1 -
9x² -6x +
9x² -6x +
Estudando o sinal de 9x² -6x +
- Determinar as raízes da equação:
9x² -6x +
Usando a Fórmula de Bkaskara, temos:
| Δ = (-6)²-4.9. Δ = 36 - 32 Δ = 4 |
Logo, as raízes da equação são :
-Graficamente:
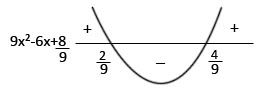
Portanto|3x-1|<
 ⇔ 9x² -6x +
⇔ 9x² -6x +  < x <
< x < e) |2x²- 1| < 1
Solução:
|2x²- 1|² < 1²
(2x²- 1)² < 1
4x4 -4x² + 1 < 1
4x4 -4x² + 1-1 < 0
4x4 -4x² < 0
Estudando o sinal de 4x4 -4x²:
- Iremos fatorar a equação para encontrar as raízes:
4x4 -4x² = 4x² .(x² - 1) - (fatoração por evidência) - Veja em Fatoração de Polinômios.
Estudo do sinal de 4x²:
- Determinar as raízes da equação:
4x² = 0
x² = 0
x = 0
Logo, as raízes de 4x² são 0.
-Graficamente:
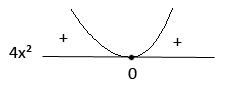
Estudo do sinal de x² - 1:
- Determinar as raízes da equação:
x² - 1 = 0
x² = 1
x = ± √1
x = ± 1
Logo, as raízes de x² - 1 são : 1 e -1.
-Graficamente:

Portanto, 4x4 -4x² = 4x² .(x - 1)(x+1) e suas raízes são 0, 1 e -1.
Graficamente:
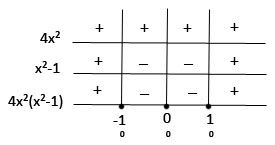
Portanto, |2x²- 1| < 1 ⇔ 4x4 -4x² < 0 ⇔ 4x² .(x² - 1) < 0 , para -1 < x < 1, x ≠ 0 , pois 4x² .(x² - 1) = 0 , se x = 0.
f) |x-3| < 4
Solução:
|x-3|² < 4²
(x-3)² < 16
x² -6x +9 < 16
x² -6x +9 -16 <0
x² -6x -7 <0
Estudando o sinal de x² -6x -7:
- Determinar as raízes da equação:
x² -6x -7 = 0
Usando a Fórmula de Bkaskara, temos:
| Δ = (-6)²-4.1.(-7) Δ = 36+28 Δ = 64 |
Logo, as raízes da equação são : 7 e -1.
-Graficamente:
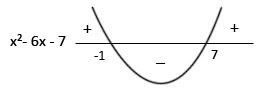
Portanto, |x-3| < 4 ⇔ x² -6x -7 <0 , para -1 < x < 7.
g) |x| > 3
Solução:
|x|² > 3²
x² >9
x² - 9 >0
Estudando o sinal de x² - 9:
- Determinar as raízes da equação:
x² - 9 = 0
x² = 9
x = ± √9
x = ± 3
Logo, as raízes da equação são : 3 e -3.
-Graficamente:
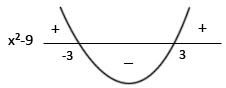
Portanto, |x| > 3 ⇔ x² - 9 >0 , para x < -3 ou x > 3.
h) |x + 3| > 1
Solução:
|x + 3|² > 1²
(x + 3)² > 1
x² +6x +9 > 1
x² +6x +9 -1>0
x² +6x +8>0
Estudando o sinal de x² +6x +8:
- Determinar as raízes da equação:
x² +6x +8 = 0
Usando a Fórmula de Bkaskara, temos:
| Δ = 6²-4.1.8 Δ = 36-32 Δ = 4 |
Logo, as raízes da equação são : -2 e -4.
-Graficamente:
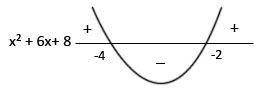
Portanto, |x + 3| > 1 ⇔ x² +6x +8 >0 , para x < -4 ou x > -2.
i) |2x – 3| > 3
Solução:
|2x – 3|² > 3²
(2x – 3)² > 9
4x² -12x +9 > 9
4x² -12x +9 -9 >0
4x² -12x >0
Estudando o sinal de 4x² -12x:
- Iremos fatorar a equação para encontrar as raízes:
4x² -12x = 4x.(x-3) - (fatoração por evidência) - Veja em Fatoração de Polinômios.
Sabemos que : ax² + bx +c = a.(x - x1)(x - x2), logo 4x² -12x = 4.(x-0)(x-3), portanto suas raízes são 0 e 3.
-Graficamente:
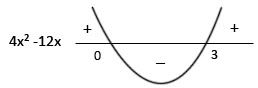
Portanto, |2x – 3| > 3 ⇔ 4x² -12x >0 , para x < 0 ou x > 3.
j) |2x – 1| < x
Solução:
|2x – 1|² < x²
(2x – 1)² < x²
4x² -4x + 1 < x²
4x² -4x + 1 -x² <0
3x² -4x + 1 <0
Estudando o sinal de 3x² -4x + 1:
- Determinar as raízes da equação:
3x² -4x + 1 = 0
Usando a Fórmula de Bkaskara, temos:
| Δ = (-4)²-4.3.1 Δ = 16-12 Δ = 4 |
Logo, as raízes da equação são : 1 e
-Graficamente:
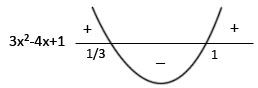
Portanto,|2x – 1| < x ⇔ 3x² -4x + 1 <0 , para
l) |x + 1| <|2x – 1|
Solução:
|x + 1|² <|2x – 1|²
(x + 1)² <(2x – 1)²
x² + 2x + 1 < 4x² -4x + 1
x² -4x² + 2x + 4x + 1-1 < 0
-3x² +6x <0
Estudando o sinal de -3x² +6x:
- Iremos fatorar a equação para encontrar as raízes:
-3x² +6x = -3x.(x-2) - (fatoração por evidência) - Veja em Fatoração de Polinômios.
Sabemos que : ax² + bx +c = a.(x - x1)(x - x2), logo -3x² +6x = -3.(x-0)(x-2), portanto suas raízes são 0 e 2.
-Graficamente (a < 0):
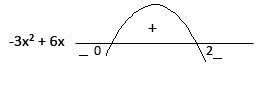
Portanto,|x + 1| <|2x – 1| ⇔ -3x² +6x <0 , x < 0 ou x > 2.
m) |x – 1| - |x + 2| > x
Solução:
Pela definição de módulo, temos:
e
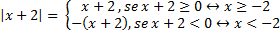
Graficamente:
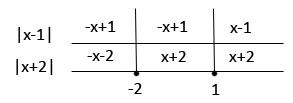
- Se x < -2
|x-1| = -x+1
|x+2| = -x-2
Assim:
|x-1|-|x+2| > x
-x+1- (-x-2) > x
-x +1 +x + 2 > x
3 > x ou x < 3
-Intersecção de x < -2 e x < 3 ,sendo A = x < -2 e B= x< 3
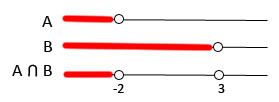
Portanto a desigualdade é válida para todo x < -2.
- Se -2 ≤ x < 1
|x-1| = -x+1
|x+2| = x+2
Assim:
|x-1|-|x+2| > x
-x+1- (x+2) > x
-x +1 -x - 2 > x
-2x-1 > x
-2x-x >1
-3x >1
3x < -1 *
x <
-Intersecção de-2 ≤ x ≤ 1 e x <
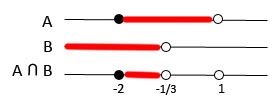
Portanto a desigualdade é válida para todo -2 ≤ x <
-Se x ≥ 1
|x-1| = x-1
|x+2| = x+2
Assim:
|x-1|-|x+2| > x
x-1- (x+2) > x
x -1 -x - 2 > x
-3 > x ou x > -3
-Intersecção de x ≥ 1 e x > -3,sendo A = x ≥ 1 e B= x > -3.
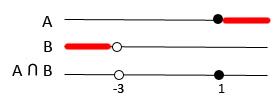
Portanto a desigualdade não é valida nesse intervalo pois não há intersecção.
Para saber para quais valores de x a inequação é válida, basta fazer a união dos intervalos em que a desigualdade é válida.
-União de A e B , sendo A = x < -2 e B= -2 ≤x <
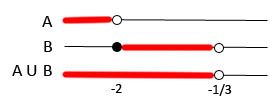
Portanto, |x – 1| - |x + 2| > x , para x <
n) |x – 3| < x + 1
Solução:
|x – 3|² < (x+1)²
(x – 3)² < (x+1)²
x² -6x +9 < x² +2x +1
x² -6x - x² - 2x < 1 - 9
-8x < -8 *
8x > 8
x >
x > 1
Portanto,|x – 3| < x + 1 , para x >1.
o) |x – 2| + |x – 1| > 1
Solução:
Pela definição de módulo, temos:
e
Graficamente:
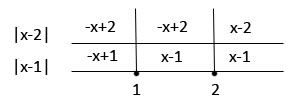
- Se x < 1
|x-2| = -x+2
|x-1| = -x+1
Assim:
|x – 2| + |x – 1| > 1
-x + 2 -x +1 > 1
-2x + 3 > 1
-2x > 1-3
-2x > -2
2x < 2 *
x <
x < 1
Portanto a desigualdade é válida para todo x < 1.
- Se 1≤ x < 2
|x-2| = -x+2
|x-1| = x-1
Assim:
|x – 2| + |x – 1| > 1
-x + 2 + x -1 > 1
1 > 1
Observe que chegamos em um absurdo (1 > 1), portanto a desigualdade não é válida nesse intervalo.
-Se x ≥ 1
|x-2| = x-2
|x-1| = x-1
Assim:
|x – 2| + |x – 1| > 1
x - 2 + x -1 > 1
2x - 3 > 1
2x > 1+3
2x > 4
x >
x > 2
Portanto a desigualdade é válida para todo x < 2.
Para saber para quais valores de x a inequação é válida, basta fazer a união dos intervalos em que a desigualdade é válida.
-União de A e B , sendo A = x < 1 e B= x > 2
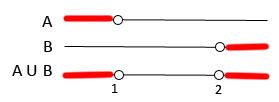
Portanto, |x – 2| + |x – 1| > 1 , para x < 1 ou x > 2.
4. Suponha r > 0. Prove:
|x| > r ⇔ x < -r ou x > r
Solução:|x|² > r²
x² > r²
x² - r² > 0
Graficamente:
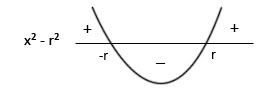
Portanto, x² - r² > 0 ⇔ |x| > r para x < -r e x > r.
5. Elimine o módulo.
a) | x + 1| + |x|
Solução:
Pela definição de módulo, temos:
e
Graficamente:
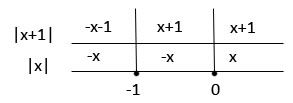
- Se x < -1
|x+1| = -x-1
|x| = -x
Assim:
| x + 1| + |x| = -x-1-x = -2x-1
- Se -1 ≤ x < 0
|x+1| = x + 1
|x| = -x
Assim:
| x + 1| + |x| = x+1-x = 1
- Se x ≥ 0
|x+1| = x + 1
|x| = x
Assim:
| x + 1| + |x| = x+1+x = 2x + 1
Portanto ,
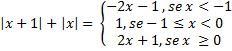
b) |x – 2| - |x + 1|
Solução:
Pela definição de módulo, temos:
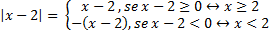
e
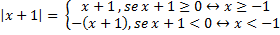
Graficamente:
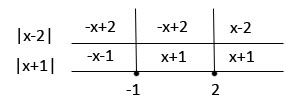
- Se x < -1
|x-2| = -x+2
|x+1| = -x-1
Assim:
|x – 2| - |x + 1| = -x+2 -(-x-1) = -x + 2 + x + 1= 3
- Se -1 ≤ x < 2
|x-2| = -x+2
|x+1| = x+1
Assim:
|x – 2| - |x + 1| = -x+2 -(x+1) = -x + 2 - x - 1= -2x+1
- Se x ≥ 0
|x-2| = x-2
|x+1| = x+1
Assim:
|x – 2| - |x + 1| = x-2 -(x+1) = x - 2 - x - 1= -3
Portanto ,
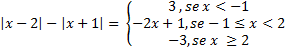
c) |2x – 1| + |x -2|
Solução:
Pela definição de módulo, temos:
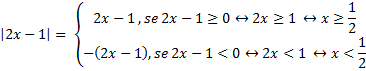
e
Graficamente:
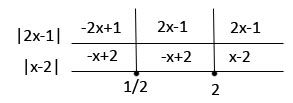
- Se x <
|2x-1| = -2x+1
|x-2| = -x+2
Assim:
|2x – 1| + |x -2| = -2x+1-x+2 = -3x + 3
- Se
|2x-1| = 2x-1
|x-2| = -x+2
Assim:
|2x – 1| + |x -2| = 2x-1-x+2 = x + 1
- Se x ≥ 2
|2x-1| = 2x-1
|x-2| = x-2
Assim:
|2x – 1| + |x -2| = 2x-1+ x-2 = 3x -3
Portanto ,
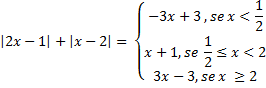
e) |x|+|x - 1|+|x - 2|
Solução:
Pela definição de módulo, temos:
e
e
Graficamente:
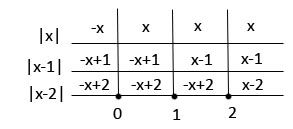
- Se x < 0
|x| = -x
|x-1| = -x+1
|x-2|= -x+2
Assim:
|x|+|x - 1|+|x - 2| = -x -x +1 -x + 2= -3x + 3
- Se 0 ≤x <1
|x| = x
|x-1| = -x+1
|x-2|= -x+2
Assim:
|x|+|x - 1|+|x - 2| = x -x +1 -x + 2= -x + 3
- Se 1 ≤x <2
|x| = x
|x-1| = x-1
|x-2|= -x+2
Assim:
|x|+|x - 1|+|x - 2| = x + x -1 -x + 2= x + 1
- Se x ≥ 2
|x| = x
|x-1| = x-1
|x-2|= x-2
Assim:
|x|+|x - 1|+|x - 2| = x + x -1 + x - 2 = 3x -3
Portanto ,
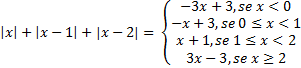
6. Prove: |x + y| = |x| + |y| ⇔ xy ≥ 0
Solução:
De acordo com a definição de módulo, temos:
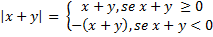
e
e
Sabemos que xy ≥ 0 , portanto nos deparamos com 5 casos :
Caso 1: Se x e y > 0 , temos xy > 0 e x + y > 0, assim:
|x + y | = x + y = | x | + | y |
Caso 2: Se x e y < 0, temos xy > 0 e x + y < 0, assim:
|x + y| = -(x + y) = -x-y = (-x) + (-y) = | x | + | y |
Caso 3: Se x = 0 , temos xy = 0
i ) se y > 0, temos x + y > 0, assim:
|x+y| = x+y = | x |+| y |
ii) se y < 0, temos x + y < 0, assim:
|x + y| = -(x + y) = -x-y = (-x) + (-y) = | x | + | y |
Caso 4: Se y = 0 , temos xy = 0
i ) se x > 0, temos x + y > 0, assim:
|x+y| = x+y = | x |+| y |
ii) se x < 0, temos x + y < 0, assim:
|x + y| = -(x + y) = -x-y = (-x) + (-y) = | x | + | y |
Caso 5: Se x = 0 e y =0, temos xy = 0 e x + y = 0, assim:
|x + y| = x + y = | x |+| y |
Portanto, |x + y| = |x| + |y| ⇔ xy ≥ 0, para todo x e y.
7. Prove:
Dica :
-Propriedades úteis:
i) | x | ≥ 0
ii ) |x| ² = x²
iii) |xy| = |x||y|
a) | x – y| ≥ |x| - |y|
Solução :
Elevando ambos os membros da desigualdade ao quadrado, temos:
| x - y |² ≥ (|x| - |y|)²
( x - y )² ≥ (|x| - |y|)²
x² - 2xy + y² ≥ |x|² - 2|x||y| + |y|²
x² - 2xy + y² ≥ x² - 2|x||y| + y²
x² -x² - 2xy + y² -y² ≥ - 2|x||y|
- 2xy ≥ - 2|x||y|
Sendo |x||y| = |x.y| e |xy| ≥ 0,de acordo com as propriedades (iii) e (i), temos que -2|x||y| ≤ 0, para qualquer x e y, logo - 2xy ≥ - 2|x||y| .
b) |x – y| ≥ |y| - |x|
Solução:
Elevando ambos os membros da desigualdade ao quadrado, temos:
| x - y |² ≥ (|y| - |x|)²
( x - y )² ≥ (|y| - |x|)²
x² - 2xy + y² ≥ |y|² - 2|y||x| + |x|²
x² - 2xy + y² ≥ y² - 2|y||x| + x²
x² -x² - 2xy + y² -y² ≥ - 2|y||x|
- 2xy ≥ - 2|y||x|
Sendo |y||x| = |y.x| e |yx| ≥ 0,de acordo com as propriedades (iii) e (i), temos que -2y||x| ≤ 0, para qualquer x e y, logo - 2xy ≥ - 2|y||x|.
c) ||x|-|y|| ≤ |x - y|
Solução:
Elevando ambos os membros da desigualdade ao quadrado, temos:
||x|-|y||² ≤ |x - y|²
(|x|-|y|)² ≤ (x - y)²
|x|² - 2|x||y| + |y|² ≤ x² -2xy + y²
x² - 2|x||y| + y² ≤ x² -2xy + y²
x² -x² - 2|x||y|+ y² -y² ≤ -2xy
- 2|x||y| ≤ -2xy
Sendo |y||x| = |y.x| e |yx| ≥ 0,de acordo com as propriedades (iii) e (i), temos que -2|x||y| ≤ 0, para qualquer x e y, logo - 2|x||y| ≤ -2xy .
_____________________________________________________________________
Formula de Bhaskara : é a nome que se dá a fórmula usada na resolução de equações do segundo grau.
| Δ = b² - 4ac | e |
* Ao multiplicarmos ambos os lados por um número negativo o sinal de desigualdade se invertee. Veja:
- 3x < 5
-3x (-1) < 5 (-1)
3x > -5
muito bom este seu blog espero que der continuidade a esta resolução que vem salvando alunos desesperados como eu :)
ResponderExcluirobrigada Manoel.! que bom que está ajudando.!
Excluircontinuarei sim, é que agora está tudo meio corrido mas continuarei assim que puder.!
=D
tomara que dê certo, pois essas resoluçoes sao muito boas
Excluircaramba, muito obrigado mesmo!rs
ResponderExcluirnossa por favor estou precisando urgentimente da resolução dos exercicios de função... vc poderia me ajudar
ResponderExcluirOla thpp, eu não tenho os exercícios resolvidos, mas me mande os que você não conseguir fazer que eu te ajudo.
Excluiremail: pcommerce92@gmail.com
eu ja te mandei o email..
ExcluirMto obrigado pela atenção, e por ter me respondido..
Ola, eu preciso dos exercícios do capitulo 3 e 4! Se puder me ajudar! Obg!
ResponderExcluirEssas propagandas esta tampando as respostas
ResponderExcluirMuito bom! Pena que não teve continuidade...
ResponderExcluirGostei muito.amei....
ResponderExcluirGostaria que tivesse continuidade, pois assim aprendir melhor, pois as vezes o professor na graduação não tem paciência de ensinar detalhadamente.
ResponderExcluirna questão 3, alternativa B, como chegou no 4x após realizar a distributiva (2x-1)^2??
ResponderExcluirMuito Obrigado
ResponderExcluirMEU NOBRE!!!! BOA TARDE!!!! DISPONIBILIZE O SEU PIX PARA PODERMOS CONTRIBUIR COM SEU TRABALHO DE DIVULGAR DE FORMA EFICIENTE PARA AJUDAR OS DEMAIS ESTUDANTES!!!! FICAREI AGUARDANDO SUA RESPOSTA!!!! VALEU!!!!
ResponderExcluir